Parser

Der Parser analysiert die Liste der Tokens anhand einer gegebenen Syntax und erstellt eine Baumstruktur („Abstract Syntax Tree“), die die Bedeutung („Semantik“) des Programmtextes wiedergibt. Die Syntax unserer einfachen Beispielsprache entspricht der einfacher mathematischer Terme:

• Eine Summe besteht aus dem linken Summanden gefolgt vom Zeichen + gefolgt vom rechten Summanden
• Entspechend mit Produkt, Differenz und Quotient
• Es gilt „Punkt vor Strich“
• Teilterme in Klammern werden zuerst berechnet.
• Steht ein Minuszeichen vor einem Term, so wird der Termwert mit -1 multipliziert (Negation)

Wie man eine solche Syntax besser aufschreibt (Backus-Naur-Form) beschreibe ich später. Für das Verständnis des Compilers reicht die Beschreibung oben.

Aus dem Term 1 + 2 * (4 * -a1 - 3) macht der Lexer folgende Tokens:

zahl[1.0] plus zahl[2.0] mal klammerAuf zahl[4.0] mal minus text[a1] minus zahl[3.0] klammerZu

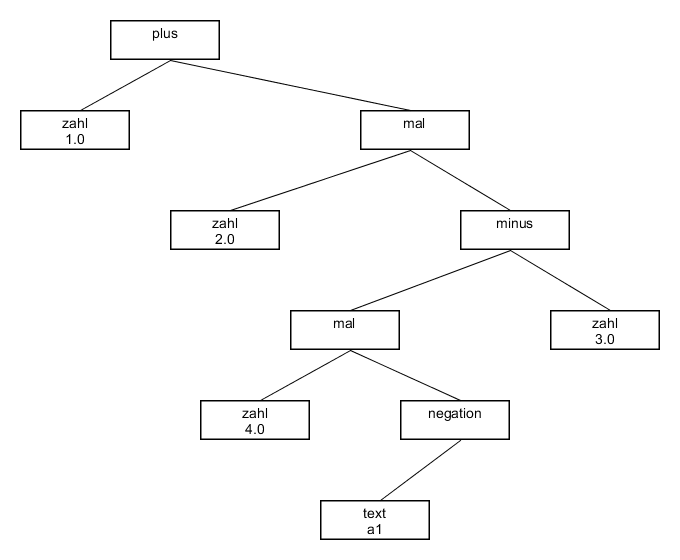
Man beachte, dass der Lexer noch nicht zwischen einer Differenz (zweites „minus“) und einer Negation (erstes „Minus“) unterscheiden kann. Der Parser erzeugt aus der Liste von Tokens folgende Baumstruktur:

Die rechteckig umrahmten Teile des Baums nennt man Knoten, die Verbindungslinien Kanten. Der Knoten ganz oben heißt Wurzel. Der Baum wird traditionell mit der Wurzel nach oben gezeichnet, da man beim Zeichnen auf Papier anfangs nicht weiß, wie hoch der Baum wird. Für unsere einfache Programmiersprache hat jeder Knoten maximal 2 Kanten, wir können die Knoten also durch folgende klasse abbilden:

public class Knoten {
 
	/**
	 * Im Token steckt der Inhalt des Knotens drin, also ein Operator, eine Zahl oder ein 
	 * Variablenbezeichner. Der Einfachheit halber verwenden wir hier die Klasse Token. 
	 */
	private Token token; 
 
	/**
	 * Kindknoten linkerhand
	 */
	private Knoten links;
 
	/**
	 * Kindknoten rechterhand
	 */
	private Knoten rechts;
 
	public Knoten(Token token) {
		super();
		this.token = token;
	}
 
	public Knoten(Token token, Knoten linkerOperand, Knoten rechterOperand) {
		this.token = token;
		this.links = linkerOperand;
		this.rechts = rechterOperand;
	}
 
	public Knoten getLinks() {
		return links;
	}
 
	public void setLinks(Knoten links) {
		this.links = links;
	}
 
	public Knoten getRechts() {
		return rechts;
	}
 
	public void setRechts(Knoten rechts) {
		this.rechts = rechts;
	}
 
	public Token getToken() {
		return token;
	}
 
}

Will man auf einen Baum im Programm zugreifen, so reicht es, seine Wurzel in einem Attribut zu speichern. Durch sukzessiven Aufruf von getRechts() und getLinks() bekommt man jeden beliebigen Knoten unterhalb.

Es gibt verschiedene Arten, einen Parser zu programmieren. Die einfachste, „von Hand“ machbare Art ist ein recursive descent parser. Um die Idee dahinter zu begreifen, geht man im konkreten Beispiel von folgender Deutung der Syntax aus:

• Eine Summe besteht aus
  • einem Produkt/Quotienten (=linker Summand), einem Pluszeichen und einem weiteren Produkt/Quotienten (rechter Summand) oder
  • ausschließlich aus einem Produkt/Quotienten
• Ein Produkt besteht aus
  • einem „einfachen Term“ (=linker Faktor), einem Malzeichen und einem weiteren „einfachen Term“ (rechter Faktor) oder
  • ausschließlich aus einem „einfachen Term“.
• Analog mit Differenz bzw. Quotient
• Ein „einfacher Term“ besteht aus
  • einer öffnenden Klammer, einer Summe(bzw. Differenz) und einer schließenden Klammer oder
  • einem Minuszeichen gefolgt von einem „einfachen Term“ oder
  • einer Variablen oder
  • einer Zahl.

Bem.: In dieser Beschreibung steckt implizit schon drin, dass „Punkt vor Strich“ gilt.

Obiger Beschreibung folgend ruft die Methode summeDifferenz() zunächst die Methode produktQuotient() auf, um den ersten Summanden (bzw. Minuend) zu ermitteln. Folgt danach ein + oder ein -, so handelt es sich um eine „echte“ Summe/Differenz und es wird anschließend nochmals produktQuotient aufgerufen, um den zweiten Summanden (bzw. den Subtrahenden) zu parsen. Folgt weder ein + noch ein Minus, so besteht die komplette Summe nur aus einem Produkt.
Falls eine echte Summe vorliegt, kann diese natürlich wiederum der erste Summand einer weiteren Summe sein (1 + 2 ist der erste Summand von 1 + 2 + 3. Daher wird in ersterem Fall am Ende überprüft, ob nochmals ein + oder - vorliegt und ggf. das ganze wiederholt.

Die Methode produktQuotient() ist ganz analog zu summeDifferenz() programmiert. Sie sucht als ersten Summanden einen einfachen Term, …

Insgesamt erkennt man am Vorgehen die Namensgebung: Durch rekursive Aufrufe („recursive“) parst man die Tokenliste und erzeugt absteigend („descent“) den Parse-Baum (Abstract Syntax Tree).

Die Einzelheiten der Programmierung kann man am besten am kommentierten Sourcecode ersehen.

Hier der Sourcecode der Klasse Parser.

package parser;
 
import java.util.ArrayList;
 
import lexer.Token;
import lexer.TokenType;
 
public class Parser {
 
	/**
	 * Liste, die vom Lexer kommt
	 */
	private ArrayList<Token> tokenListe;
 
	/**
	 * Zur Speicherung des Parse-Baums (Abstract Syntax Tree) reicht es, die
	 * Wurzel zu speichern. Über sie bekommt man jeden beliebigen Knoten
	 * darunter.
	 */
	private Knoten wurzel;
 
	/**
	 * Nummer des Tokens, das gerade analysiert wird (von 0 beginnend)
	 */
	private int position;
 
	/**
	 * 
	 * @param tokenListe
	 *            Liste von Tokens, die geparst werden soll
	 */
	public Parser(ArrayList<Token> tokenListe) {
 
		super();
 
		this.tokenListe = tokenListe;
 
		position = 0;
 
	}
 
	/**
	 * Parst die dem Konstruktor übergebene Liste von Tokens und gibt einen
	 * Parse-Baum (Abstract Syntax Tree) zurück.
	 * 
	 * @return Parse-Baum (Abstract Syntax Tree)
	 * @throws Exception
	 *             Falls die Liste der Tokens nicht der Syntax entspricht
	 */
	public Knoten parse() throws Exception {
 
		wurzel = summeDifferenz(); // Versuche, eine Summe oder Differenz zu finden
 
		return wurzel;
 
	}
 
	/**
	 * Versucht, eine Summe oder Differenz zu parsen. Parst zunächst den ersten
	 * Operanden (unter der Annahme, dass es eine Multiplikation oder Division
	 * ist) und sieht dann nach, ob ein Pluszeichen oder ein Minuszeichen kommt.
	 * Falls "ja", parst es den zweiten Operanden und fügt alle drei zu einem
	 * Baum zusammen.
	 * 
	 * Folgt ein weiteres Plus oder Minus, wird der Baum als erster Operand
	 * einer weiteren Summe/Differenz gedeuet und nach dem zweiten Operanden
	 * dazu gesucht usw.
	 * 
	 * Folgt kein weiteres Plus oder Minus, so endet die Methode und der
	 * aktuelle Baum wird zurückgegeben.
	 * 
	 * @return Geparster Teilbaum
	 * @throws Exception
	 */
	private Knoten summeDifferenz() throws Exception {
 
		Knoten linkerOperand = produktQuotient(); // Versuche, eine Multiplikation
												// oder Division zu finden
 
		while (peek() == TokenType.plus || peek() == TokenType.minus) {
 
			Token operator = nextToken();
 
			Knoten rechterOperand = produktQuotient();
 
			Knoten neuerKnoten = new Knoten(operator, linkerOperand,
					rechterOperand);
 
			linkerOperand = neuerKnoten;
 
		}
 
		return linkerOperand;
 
	}
 
	/**
	 * Wie PlusMinus, jedoch für Mal und geteilt. Als erster bzw. zweiter
	 * Operand wird nach einem einfachen Term (Klammerterm, Zahl, Variable oder
	 * Negation) gesucht.
	 * 
	 * @return
	 * @throws Exception
	 */
	private Knoten produktQuotient() throws Exception {
 
		Knoten linkerOperand = einfacherTerm();
 
		while (peek() == TokenType.mal || peek() == TokenType.geteilt) {
 
			Token operator = nextToken();
 
			Knoten rechterOperand = einfacherTerm();
 
			Knoten neuerKnoten = new Knoten(operator, linkerOperand,
					rechterOperand);
 
			linkerOperand = neuerKnoten;
 
		}
 
		return linkerOperand;
 
	}
 
	private Knoten einfacherTerm() throws Exception {
 
		if (peek() == null) {
			throw new Exception("Parserfehler: unerwartetes Ende");
		}
 
		switch (peek()) {
		case klammerAuf: // Klammerterm
			nextToken();
			Knoten knoten = summeDifferenz(); // In der Klammer kann sich wieder eine
											// Summe/Differenz befinden...
			erwarte(TokenType.klammerZu); // Überliest die schließende Klammer
			return knoten;
		case text:
			return new Knoten(nextToken());
		case zahl:
			return new Knoten(nextToken());
		case minus:
			Knoten knoten1 = new Knoten(new Token(TokenType.negation));
			nextToken(); // überliest das Minuszeichen
			knoten1.setLinks(einfacherTerm()); // die Negation wirkt auf den einfachen
										// Term danach
			return knoten1;
		default:
			throw new Exception("Das Token " + peek() + " ist fehl am Platz.");
		}
 
	}
 
	/**
	 * Gibt das nächste Token aus der Tokenliste zurück, erhöht aber nicht die
	 * Leseposition
	 * 
	 * @return
	 */
	public TokenType peek() {
 
		if (position < tokenListe.size()) {
 
			return tokenListe.get(position).getTokenType();
 
		}
 
		return null;
	}
 
	/**
	 * Gibt das nächste Token aus der Tokenliste zurück und erhöht(!) die
	 * Leseposition
	 * 
	 * @return
	 */
	public Token nextToken() {
 
		if (position < tokenListe.size()) {
 
			Token token = tokenListe.get(position);
 
			position++;
 
			return token;
 
		}
 
		return null;
 
	}
 
	/**
	 * Wirft eine Exception, wenn das nächste Token in der Tokenliste nicht dem
	 * übergebenen Typ entspricht.
	 * 
	 * @param tokenType
	 * @throws Exception
	 */
	public void erwarte(TokenType tokenType) throws Exception {
 
		if (peek() == null) {
			throw new Exception(
					"Parserfehler: unerwartetes Ende. Erwartet wird: "
							+ tokenType);
		}
 
		if (peek() != tokenType) {
			throw new Exception("Parserfehler: Erwartet wird: " + tokenType);
		}
 
		nextToken();
 
	}
 
	/**
	 * Nur zu Debuggingzwecken
	 */
	@Override
	public String toString() {
 
		StringBuilder sb = new StringBuilder();
 
		toString(wurzel, "", sb);
 
		return sb.toString();
 
	}
 
	/**
	 * Traversiert vom übergebenen Knoten ausgehend den Teilbaum in pre-order
	 * Reihenfolge, d.h. zuerst wird der Konten selbst besucht, dann der
	 * komplette linke Teilbaum, der dranhängt, dann der komplette rechte
	 * Teilbaum, der dranhängt.
	 * 
	 * @param knoten
	 * @param einruecken
	 * @param sb
	 */
	private void toString(Knoten knoten, String einruecken, StringBuilder sb) {
 
		sb.append(einruecken);
		sb.append(knoten.getToken().toString() + "\n");
 
		if (knoten.getLinks() != null) {
			toString(knoten.getLinks(), einruecken + "   ", sb);
		}
 
		if (knoten.getRechts() != null) {
			toString(knoten.getRechts(), einruecken + "   ", sb);
		}
 
	}
 
	public Knoten getWurzel() {
		return wurzel;
	}
 
}

Hier geht's weiter zur Beschreibung des Interpreters.